6. Waagerechter Wurf

Bezugssysteme

Zur Beschreibung von Bewegungen benötigt man zu jedem Zeitpunkt Kenntnis über den Ort eines Körpers. Die Ortskoordinaten werden bezüglich eines geeignet gewählten Koordinatensystems bestimmt. Beispiele:

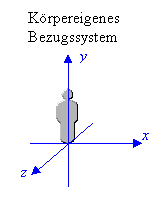
Im allgemeinen wird die Bewegung eines Körpers in verschiedenen Bezugssystemen auch unterschiedlich beschrieben.

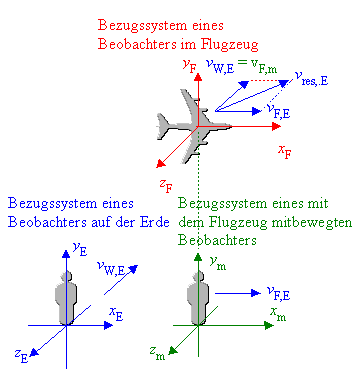
Beispiel:Ein auf der Erdoberfläche ruhender Beobachter beobachtet ein Flugzeug, dass sich längs der x-Achse des Bezugssystems des Beobachters bewegt. Dieser Beobachter registriert die Flugzeuggeschwindigkeit v_F,E.

Für einen im Flugzeug befindlichen Beobachter, der ein mit dem Flugzeug verbundenes Koordinatensystem benutzt, ist das Flugzeug in Ruhe: v_F,F = 0.

Ein Beobachter, der sich auf der Erdoberfläche mit dem Flugzeug mitbewegt, registriert in seinem Bezugssystem ebenfalls die Flugzeuggeschwindigkeit v_F,m = 0.

Für den ruhenden Beobachter bewegt sich der mit dem Flugzeug mitbewegte Beobachter natürlich auch mit der Geschwindigkeit v_m,E = v_F,E in x_E-Richtung.

Nun soll zusätzlich ein Seitenwind berücksichtigt werden, der im Bezugssystem des ruhenden Beobachters in –z_E- Richtung mit der Geschwindigkeit v_W,E weht und dem Flugzeug diese Geschwindigkeit in –z_E-Richtung erteilt.

Für den auf der Erdoberfläche befindlichen bewegten zweiten Beobachter erhält das Flugzeug dadurch die Geschwindigkeit v_F,m = v_W,E. in –z_m-Richtung.

Der ruhende Beobachter dagegen registriert die Überlagerung der Flugzeugbewegung in x_E-Richtung und in –z_E-Richtung. Für ihn bewegt sich das Flugzeug nun in Richtung der resultierenden Geschwindigkeit, die durch die Vektorsumme

gegeben ist.

Versuch

Es soll eine kleine Kugel mittels eines Wurfgerätes waagerecht abgeworfen werden. Das Koordinatensystem zur Beschreibung der Bewegung der Kugel hat seinen Ursprung im Abwurfpunkt (Unterkante Kugel).

Vorversuch:

Das Wurfgerät wird auf einer Stativstange befestigt.

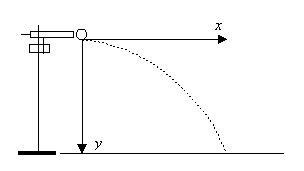
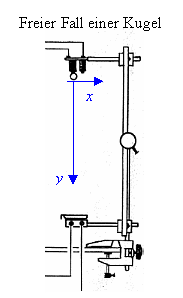
Der Probekörper (Kugel) wird waagerecht abgeschossen. Im Moment des Abschusses wird gleichzeitig ein zweiter Probekörper (Kugel) aus der Höhe, in der der erste Körper abgeschossen wird, senkrecht fallen gelassen. Zu beobachten ist, dass beide Körper gleichzeitig auf dem Boden ankommen.

Deutung:

Das gleichzeitige Auftreffen auf dem Boden ist nur möglich, wenn für beide Kugeln die Fallbewegung in genau gleicher Weise erfolgt. Der Versuch zeigt, dass die senkrechte Fallbewegung nicht von der gleichzeitig erfolgenden Bewegung in horizontaler Richtung beeinflusst wird. Beide Teilbewegungen erfolgen offenbar völlig unabhängig voneinander. Die reale Bewegung setzt sich zusammen aus zwei voneinander unabhängigen Teilbewegungen.

Messung:

Es werden verschiedene Fallstrecken y eingestellt und die zugehörige Wurfweite x gemessen. Auf diese Weise ergeben sich mehrere Punkte (x ; y) der Bahnkurve, die der waagerecht abgeworfene Körper beschreibt.

Auswertung:

x-y-Diagramm der Bahnpunkte:

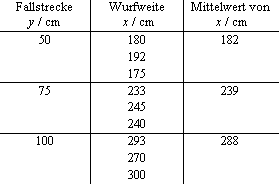
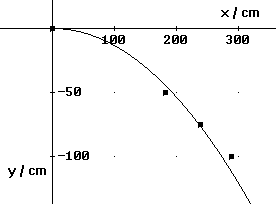
Die Bahnpunkte könnten auf einer Parabel liegen. Zur Überprüfung wird der Quotient gebildet:

Es gilt also näherungsweise

Diese Parabel ist im obigen Diagramm eingetragen.

Theorie

Wurfparabel

Beim waagerechten Wurf wird ein Körper mit der Anfangsgeschwindigkeit v₀ in x-Richtung abgeworfen. In x-Richtung wirken danach keine Kräfte mehr auf den Körper, so dass er eine gleichförmige Bewegung in dieser Richtung ausführt:

In y-Richtung wirkt die Gewichtskraft auf den Körper. Wenn der Luftwiderstand vernachlässigt werden kann, ist die Bewegung in y-Richtung ein freier Fall:

Aus der Gleichung für x ergibt sich

Wird dies in die Gleichung für y eingesetzt, so folgt

Die Bahnkurve ist also eine Parabel – die Wurfparabel.

Im Versuch wurde der Faktor vor x² bestimmt:

Vergleich mit der Gleichung der Wurfparabel zeigt:

Daraus ergibt sich die Anfangsgeschwindigkeit:

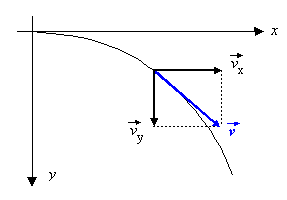
Geschwindigkeit längs der Wurfbahn

Der waagerechte Wurf setzt sich – wie beschrieben – aus der Überlagerung einer gleichförmigen Bewegung in x-Richtung und einem freien Fall in y-Richtung zusammen. Die Geschwindigkeiten v_x = v₀ und v_y = gt müssen vektoriell zur Gesamtgeschwindigkeit addiert werden:

Der Betrag der resultierenden Geschwindigkeit ergibt sich aus dem Satz des Pythagoras:

Übungen

1. a) Zeichnen Sie die Bahn des waagerechten Wurfs mit der Anfangsgeschwindigkeit im Maßstab 1 : 1000 für den Zeitabschnitt t = 0 ... 5 s. Verwenden Sie zur Vereinfachung der Zahlenwerte die Näherung.

b) Zeichnen Sie die Geschwindigkeitsvektoren für die Zeiten t₁ = 2,0 s und t₂ = 4,0 s ein (Geschwindigkeitsmaßstab: ).

c) Berechnen Sie den Betrag der Gesamtgeschwindigkeit v zu den Zeiten t₁ und t₂.

2. Ein unerfahrener Pilot lässt einen Versorgungssack genau senkrecht über dem Zielpunkt aus dem in 500 m Höhe fliegenden Flugzeug fallen. Der Sack schlägt 1,0 km vom Ziel entfernt auf. Welche Geschwindigkeit hat das Flugzeug und mit welcher Geschwindigkeit erreicht der Sack den Boden? (g = 9,81 m/s²; vom Luftwiderstand soll abgesehen werden)

3. Bei y₁ = 80 m Falltiefe kommt ein mit v₀ = 75 m/s waagerecht abgeworfener Körper x₁ = 303 m weit. Wie weit geht der Wurf bei der Falltiefe y₂ = 350 m? (g = 9,81 m/s²)

Weitere Übungen

(Für alle Aufgaben ist g = 9,81 m/s².)

1. Mit einem waagerecht gehaltenen Luftgewehr wird die Mitte einer 50 m entfernten Zielscheibe anvisiert. Das Geschoss verlässt die Mündung mit v₀ = 200 m/s. Wo trifft es auf der Zielscheibe auf?

2. Wie groß muss die Geschwindigkeit eines Tennisballs sein, der waagerecht knapp über das Netz fliegt und die Außenlinie berührt? Netzhöhe: 1,04 m; Länge einer Platzhälfte: 10,5 m.

3. Ein Wasserstrahl strömt mit 20 m/s aus einem Gartenschlauch.
a) Wie weit kann man auf ebenem Gelände damit spritzen, wenn man ihn in der Höhe 1m über dem Boden waagerecht hält?
b) In welcher Höhe müsste er gehalten werden, um 25 m weit spritzen zu können?

4. Von einem 40 m hohen Turm wird ein Stein in horizontaler Richtung mit der Anfangsgeschwindigkeit v₀ = 20 m/s abgeworfen. Mit welcher Geschwindigkeit v trifft er auf dem Boden auf?

Lösungen

1. 0,307 m unterhalb des anvisierten Punktes

2. v₀ = 82,1 km/h

3. a) x_W = 9,03 m b) h = 7, 66 m

4. v = 34,5 m/s