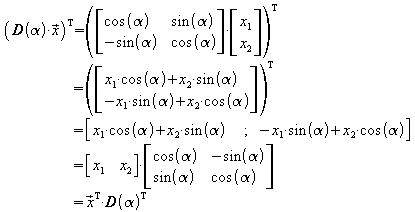1.5 Inverse Matrix, transponierte Matrix
1.5.1 Inverse Matrix
Das Koordinatensystem wird zuerst um einen Winkel
a gedreht und das gedrehte System anschließend um den Winkel -a.
Die Drehmatrix für den Winkel -a lautet:
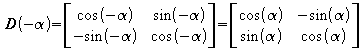 .
.
Das Produkt aus der Drehmatrix für den Winkel
a und der Drehmatrix für den Winkel -a ergibt:
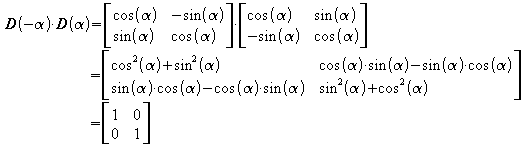 .
.
Dies ist die sogenannte Einheitsmatrix E.
Für die zwei Drehungen um a und -a folgt damit:
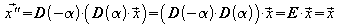 .
.
Wegen der Beziehung
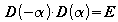
wird auch
als zu
auch
als zu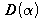 inverse
Matrix bezeichnet und als
inverse
Matrix bezeichnet und als
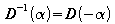
geschrieben.
1.5.2 Transponierte Matrix
Vergleicht man eine Drehmatrix und ihre inverse Matrix,
so kann man sich die inverse Matrix auch dadurch entstanden denken, dass
bei der Drehmatrix die Spalten und Zeilen vertauscht werden. Eine Matrix,
bei der Zeilen und Spalten vertauscht wurden, wird allgemein die
transponierte
Matrix genannt. Die inverse Matrix einer Drehmatrix stimmt also mit
der transponierten Matrix der Drehmatrix überein:
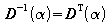 .
.
Ein (Spalten-)Vektor kann als Matrix mit zwei
Zeilen und einer Spalte aufgefasst werden. Der transponierte Vektor ist
dann eine Matrix mit einer Zeile und zwei Spalten (auch Zeilenvektor genannt).
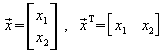 .
.
Auch ein Matrix-Vektor-Produkt, das ja einen Vektor
ergibt, kann transponiert werden:
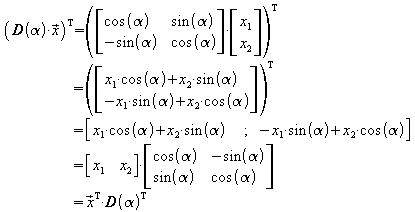
![]() .
.![]() .
.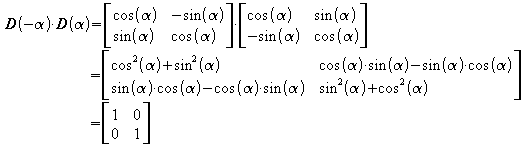 .
.![]() .
.![]()
![]() auch
als zu
auch
als zu![]() inverse
Matrix bezeichnet und als
inverse
Matrix bezeichnet und als
![]()
![]() .
.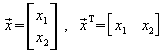 .
.