Elektromagnetische Schwingungen und Wellen

1. Elektromagnetische Schwingungen

1.1 Freie, gedämpfte elektromagnetische Schwingung

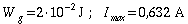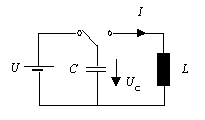
Ein Kondensator und eine Spule werden parallel geschaltet. Der Kondensator kann über einen Umschalter an eine Spannungsquelle angeschlossen werden um ihn aufzuladen.

Wird der geladene Kondensator an die Spule angeschlossen, so ist in der Spannung am Kondensator U_C und in der Stromstärke I eine Schwingung zu beobachten. Die Schwingungen von Spannung und Stromstärke sind phasenverschoben und hören schnell wieder auf.

Beispiel: Für und L = 630 H ist eine Periodendauer von etwa T = 1 s zu beobachten.

Die Parallelschaltung von Kondensator und Spule wird als elektromagnetischer Schwingkreis bezeichnet. Die von außen unbeeinflusste Schwingung, die schließlich zum Erliegen kommt, heißt freie, gedämpfte Schwingung. Zur Entstehung der Schwingung kommt es wie folgt:

• Die Energie des elektrischen Feldes des geladenen Kondensators treibt einen Strom durch die Spule und baut dort ein magnetisches Feld auf. Nach dem Lenz'schen Gesetz entsteht in der Spule eine Induktionsspannung, die dem Anstieg des Stroms entgegenwirkt.

• In dem Moment, in dem der Kondensator ganz entladen ist, erreicht die Stromstärke in der Spule ihren größten Wert; die Energie des elektrischen Feldes ist vollständig in Energie des Magnetfelds der Spule umgewandelt.

• Der entladene Kondensator kann den Strom nun nicht mehr antreiben und das Magnetfeld der Spule bricht zusammen. In der Spule entsteht nun eine Selbstinduktionsspannung, die nach dem Lenz'schen Gesetz den Strom noch eine Zeit lang in gleicher Richtung weiter treibt. Somit wird der Kondensator erneut aufgeladen, allerdings nun mit entgegengesetzter Polung. Dabei wird wieder die Energie des Magnetfelds in Energie des elektrischen Felds umgewandelt.

• In dem Moment, in dem die Stromstärke aus Null abgesunken ist, erreicht die Ladung des Kondensators wieder ihren Maximalwert, allerdings mit entgegengesetzter Polung.

• Jetzt wiederholt sich der gesamte Vorgang in umgekehrter Richtung.

Die elektromagnetische Schwingung lässt sich mit der Schwingung eines Federpendels vergleichen. Folgende Größen entsprechen einander:

1.2 Differentialgleichung der freien, ungedämpften elektromagnetischen Schwingung

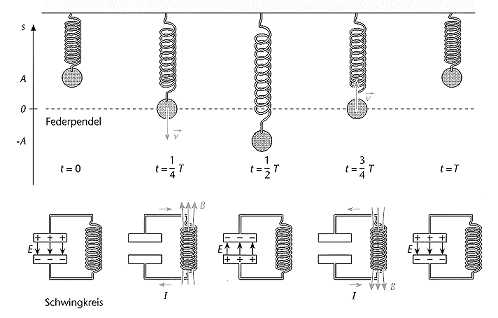
Der sich entladende Kondensator und die Spule, in der sich das Magnetfeld auf- bzw. abbaut, speisen elektromagnetische Energie in den Schwingkreis ein. Diese Energie wird im Ohm'schen Widerstand des Kreises in Wärme umgesetzt. Für die Spannungen gilt daher:

.

Wenn der Ohm'sche Widerstand vernachlässigt werden kann, liegt eine freie, ungedämpfte Schwingung vor:

.

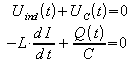Da die Ladung auf dem Kondensator abnimmt, gilt

und damit

.

Eingesetzt in die Spannungsgleichung ergibt sich

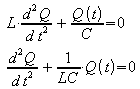
Dies ist die Differentialgleichung des harmonischen Oszillators. Die Lösung ist

.

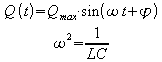Mit folgt daraus für die Eigenfrequenz und die Periodendauer des ungedämpften Schwingkreises:

.

Es soll nun speziell der Fall betrachtet werden, dass zur Zeit t = 0 der Kondensator maximal aufgeladen ist und die Entladung gerade einsetzt. Dann gilt

.

Somit muss sein, und daher . Die Zeit-Ladungs-Funktion lautet also

.

Für die Zeit-Spannungs-Funktion ergibt sich damit

,

und für die Zeit-Strom-Funktion folgt

Selbstinduktionsspannung:

Beispiel:

Periodendauer und Frequenz:

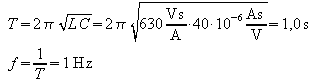
Scheitelwerte:

1.3 Energieumwandlung im Schwingkreis

Die Gesamtenergie im ungedämpften Schwingkreis setzt sich zusammen aus der Energie des elektrischen Felds im Kondensator und der Energie des magnetischen Felds in der Spule:

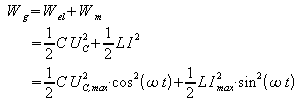
Für die maximale Stromstärke gilt

.

Damit ergibt sich für die Gesamtenergie

.

Mit

folgt

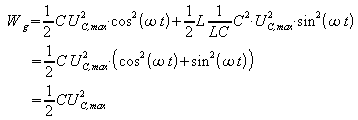
Entsprechend erhält man durch Einsetzen von

in die Gesamtenergie:

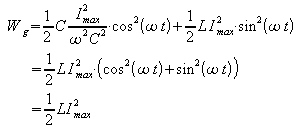
Es bestätigt sich also die Energieerhaltung:

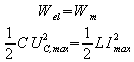
Aus dieser Beziehung ergibt sich noch ein nützlicher Zusammenhang zwischen Strom- und Spannungsamplitude:

.

1.4 Erzwungene Schwingungen und Resonanz

Aus einem Kondensator mit und einer Spule mit L = 35 mH wird ein Schwingkreis aufgebaut. Seine Eigenfrequenz ist

.

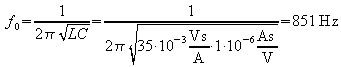Zusätzlich werden ein Tonfrequenzgenerator, der sinusförmige Spannungen veränderlicher Frequenz liefert, und ein Messwiderstand in den Kreis eingesetzt. Mit einem 2-Kanal-Oszilloskop werden die Ausgangsspannung des Tonfrequenzgenerators und die Spannung am Messwiderstand oszillographiert. Die Spannung an R_m ist ein Maß für den Strom im Schwingkreis.

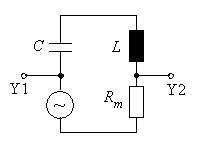
Beobachtungen:

1. Der Strom im Schwingkreis schwingt stets mit der Frequenz der Spannung des Tonfrequenzgenerators. Der Schwingkreis wird „gezwungen“, mit einer anderen Frequenz als seiner Eigenfrequenz zu schwingen. Eine solche Schwingung, die durch äußere Einwirkung hervorgerufen wird, heißt erzwungene Schwingung.

2. Der Scheitelwert I_max ändert sich mit der Frequenz der erzwungenen Schwingung. Der größte Wert tritt auf, wenn die Anregungsfrequenz mit der Eigenfrequenz des Schwingkreises übereinstimmt. Diese Übereinstimmung der Frequenzen wird Resonanz genannt.

Messung der Resonanzkurve I_max(f):

Ein Schwingkreis kann auch indirekt, über ein magnetisches Wechselfeld zu erzwungenen Schwingungen angeregt werden.

Daten: n₁ = 1200; n₂ = 12000; L₂ = 2,6 H; C = 500 pF
Eigenfrequenz des Kreises aus L₂C: f₀ = 4,4 kHz

Beobachtungen: Auch hier schwingt der Schwingkreis stets mit der Zwangsfrequenz des Tonfrequenzgenerators. Resonanz tritt wieder bei der Eigenfrequenz f₀ auf.

Übungen

1. a) Von einem Schwingkreis kennt man die Periodendauer T = 0,002 s und die Kapazität des Kondensators . Bestimmen Sie die Induktivität der Spule.
b) In einem Schwingkreis ist L = 0,04 H und die Frequenz f = 7 kHz. Bestimmen Sie die Kapazität des Kondensators.

2. In einem ungedämpften elektrischen Schwingkreis der Eigenfrequenz f = 1 kHz besitzt zum Zeitpunkt t = 0s der Kondensator der Kapazität C = 10 nF die maximale Ladung .
a) Berechnen Sie die Induktivität des Kreises.
b) Wie groß ist die Ladung des Kondensators zu den Zeitpunkten t₁=T/8 ; t₂ = T/4 ; t₃ = T/2 ; t₄ = 3T/4 ?
c) Bestimmen Sie für die angegebenen Zeiten die jeweilige Stromstärke im Schwingkreis.
d) Nach welcher Zeit ist die Stromstärke erstmalig I_max/6 ?

3. Ein Schwingkreis soll auf die Frequenz der technischen Wechselspannung abgestimmt werden.
Die Schwingkreisspule besitzt n = 3600 Windungen, eine Länge l = 0,08 m und einen Durchmesser d = 5,6 cm. Ein Eisenkern in der Spule vergrößert ihre Induktivität um den Faktor 170. Berechnen Sie die Kapazität des parallel zur Spule geschalteten Kondensators.

4. a) Welche Kapazität C besitzt der Plattenkondensator eines im Vakuum ungedämpft schwingenden Schwingkreises (f = 1 kHz), wenn die zum Kondensator parallel geschaltete Spule eine Induktivität L = 0,6 mH besitzt?
b) Zwischen die Platten des Kondensators wird ein Isolator mit der Dielektrizitätszahl gebracht. Wie verändert sich die Frequenz der ungedämpften Schwingung?

5. In einem ungedämpften Schwingkreis beträgt die Kapazität des Kondensators und die Induktivität der Spule L = 0,1 H.
a) Bestimmen Sie die Kreisfrequenz w, die Frequenz f und die Schwingungsdauer T des Kreises.
b) Berechnen Sie die Gesamtenergie und die Stromamplitude, wenn die maximale Spannung 200 V beträgt.

Lösungen

1. a) 0,34 H
    b) 12,9 nF

2. a) 2,5 H
    b)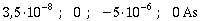
    c) 22,3 ; 31,6 ; 0 ; -31,6 mA
    d) 0,027 ms

3. 119 nF

4. a)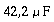
    b) Abnahme auf 461 Hz

5. a)
    b)