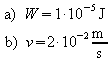.
.
Die Hubarbeit lässt sich dann mit dem Potential wie folgt beschreiben:
.
Im elektrischen Feld erhält man analog eine von der Ladung Q eines Probekörpers unabhängige Größe, die nur das Feld beschreibt: Dazu wird der Quotient von potentieller Energie und Ladung der Probeladung, die sich im Feld befindet, gebildet:
.
Diese Feldgröße wird als elektrostatisches Potential bezeichnet. Seine Einheit ist
.
Für den im Abschnitt 2.4 betrachteten Plattenkondensator und die Wahl des Nullpunkts der potentiellen Energie auf der negativen Platte gilt dann:
.
 |
Die Verschiebungsarbeit, die beim
Verschieben einer Probeladung im Feld verrichtet wird, lässt sich
mit dem Potential ausdrücken:
|
 |
Punkte im Innern des Plattenkondensators,
die die gleiche x-Koordinate besitzen, liegen auf Flächen,
die parallel zu den Kondesatorplatten liegen. Auf solchen Flächen
hat das Potential 
überall den gleichen Wert. Man nennt solche Flächen Äquipotentialflächen
(Flächen gleichen Potentials).
Wird eine Ladung auf einer Äquipotentialfläche
bewegt, ändert sich ihre potentielle Energie |
Mit der Potentialdifferenz wird eine weitere Feldgröße
gebildet:
| Definition:
Die elektrische Spannung zwischen zwei Punkten P1 und
P2 im elektrischen Feld ist gleich der Potentialdifferenz zwischen
diesen zwei Punkten:
Maßeinheit:
|
An einen Plattenkondensator mit Plattenabstand
d werde eine Gleichspannungsquelle mit der Spannung U so
angeschlossen, dass die rechte Platte positiv geladen ist. Der Nullpunkt
des Potentials wird wieder auf die linke, negativ geladene Platte gelegt:
.
Das Potential eines Punktes auf der rechten, positiv geladenen Platte beträgt
dann 
.
Die Spannung zwischen den Platten ist damit
.
Daraus ergibt sich der schon experimentell ermittelte Zusammenhang: Liegt an einem Plattenkondensator mit dem Plattenabstand d die Spannung U zwischen den Platten an, so beträgt die Feldstärke im Innern des Kondensators
.
Für die Einheit der Feldstärke ergibt sich daraus
.
Unter Berücksichtigung der Definition der Einheit V wird dies zu
.
Beispiel:
Zwischen zwei Kondensatorplatten mit d = 2,0 cm Abstand liegt die Spannung U = 1,0 kV. In das Feld zwischen den Platten wird eine Probeladung q = 10 nC gebracht.
a) Die Feldstärke beträgt
.
b) Die Kraft auf die Probeladung ist
.
c) Um die Probeladung von der negativen zur positiven Platte zu transportieren, muss folgende Verschiebungsarbeit verrichtet werden:
.
Dies ist auch gleich der potentiellen Energie der Probeladung in einem Feldpunkt mit x = d.
d) Der Verlauf des Potentials und die Lage der Äquipotentialflächen soll dargestellt werden. Dazu wird angenommen, dass sich die positive Platte rechts bei x = d und die negative Platte links bei x = 0 befindet.
Der Nullpunkt des Potentials wird wieder auf die negative Platte gelegt, so dass gilt
.
e) Die Probeladung befindet sich an einem Feldpunkt mit der x-Koordinate x1 = 0,8 cm und wird zu einem Feldpunkt mit x2 = 1,5 cm verschoben. Dazu ist die Arbeit
zu verrichten. Um diesen Betrag nimmt die potentielle Energie der Ladung zu.
f) Die Probeladung befindet sich an einem Feldpunkt
mit dem Potential 
und wird zu einem Feldpunkt mit 
verschoben. Dazu ist die Arbeit
zu verrichten. Um diesen Betrag nimmt die potentielle Energie der Ladung zu.
g) Die Probeladung wird von einem Feldpunkt 1
zu einem Feldpunkt 2 verschoben, zwischen denen eine Spannung 
liegt. Dazu ist die Arbeit
zu verrichten. Um diesen Betrag nimmt die potentielle Energie der Ladung zu.
h) Die Probeladung wird an einen Feldpunkt mit der x-Koordinate x1 = 1,7 cm gebracht und dort frei gegeben. Unter der Wirkung der Feldkräfte wird die Ladung dann in Richtung der negativen Platte bewegt. Wenn sie einen Feldpunkt mit x2 = 0,8 cm erreicht hat, ist die Arbeit
verrichtet worden. Das negative Vorzeichen bringt
zum Ausdruck, dass die Feldkräfte die Arbeit verrichtet haben und
dass daher die potentielle Energie der Ladung um den Betrag von W12
abgenommen hat.
Übungen
| empfohlende Aufgaben
aus dem Lehrbuch |
Lösungen |
| S.187, A1 |  |
| S.187, A2 |  |
| S.187, A3 |  |
Weitere Übungen
1. An einem Plattenkondensator ist die
Spannung U = 1 000 V angelegt. Auf eine Probeladung 
wirkt eine Kraft 
.
Bestimmen Sie die Feldstärke und den Plattenabstand.
2. Berechnen Sie die Kraft F auf
eine Probeladung 
im elektrischen Feld eines Plattenkondensators mit dem Plattenabstand d
= 6 cm bei der Spannung U = 1 kV.
3. An einen Plattenkondensator wird eine
Spannung U = 1 500 V gelegt. Auf eine Probeladung 
wirkt im Kondensator eine Kraft 
.
a) Bestimmen Sie die Feldstärke und den
Plattenabstand.
b) Wie groß sind Feldstärke und Plattenabstand,
wenn die Kraft auf die Probeladung doppelt so groß ist?
4. In ein homogenes Feld der Stärke 
wird die Ladung 
gebracht.
a) Berechnen Sie die Kraft, die auf die Ladung
wirkt.
b) Welche Verschiebungsarbeit wird verrichtet,
wenn die Ladung entgegen der Feldlinienrichtung eine Strecke von 3 cm bewegt
wird?
c) Welche Potentialdifferenz besteht zwischen
dem Anfangs- und dem Endpunkt dieser Strecke?
5. Ein geladenes Kügelchen der Masse
m = 0,40 g hängt an einem 1,6 m langen Faden und wird im homogenen
Feld eines Plattenkondensators um 3,0 cm ausgelenkt. Die Spannung zwischen
den Platten beträgt bei einem Plattenabstand von 8,0 cm U =
10 kV.
a) Welche Ladung trägt das Kügelchen?
b) Welche elektrische Arbeit wird an ihm verrichtet,
wenn es sich von einer Platte zur anderen bewegt?
6. Ein geladener Wattebausch durchfällt
im Vakuum eine Spannung von 10 kV.
a) Welche Energie nimmt er dabei aus dem Feld
auf?
b) Auf welche Geschwindigkeit v wird der
Wattebausch beschleunigt, wenn er sich zu Beginn in Ruhe befand? (m
= 50 g; 
)
Lösungen
1. 
2. 
3. 
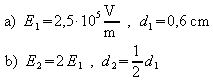
4. 
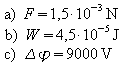
5. 
6. 
nicht. Es wird also keine Verschiebungsarbeit verrichtet. 
.