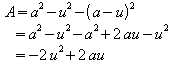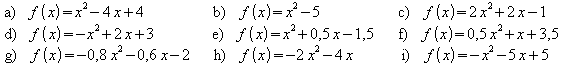5. Quadratische Funktionen
5.1 Einführung
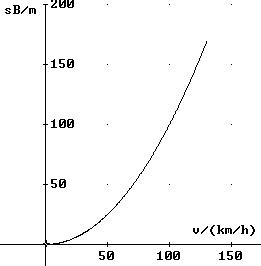
1. Eine Fahrschulregel besagt: Der Bremsweg sB
in Metern ergibt sich, indem die Geschwindigkeit v (gemessen in
km/h) durch 10 dividiert und der Quotient anschließend quadriert
wird:
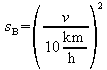 .
.
|
v / (km/h)
|
0
|
10
|
20
|
30
|
40
|
50
|
100
|
|
sB / m
|
0
|
1
|
4
|
9
|
16
|
25
|
169
|
Jeder Geschwindigkeit ist genau ein Bremsweg zugeordnet. Die Zuordnung ist
also eine Funktion; ihre Definitionsmenge ist das Intervall [0 ; vmax],
wobei vmax die Höchstgeschwindigkeit des Fahrzeugs
bezeichnet. Werden die Wertepaare (v ; sB) in
ein Koordinatensystem eingetragen, kann der Graph der Bremsweg-Funktion
gezeichnet werden.
ist
also eine Funktion; ihre Definitionsmenge ist das Intervall [0 ; vmax],
wobei vmax die Höchstgeschwindigkeit des Fahrzeugs
bezeichnet. Werden die Wertepaare (v ; sB) in
ein Koordinatensystem eingetragen, kann der Graph der Bremsweg-Funktion
gezeichnet werden.
2. Den Weg s, den ein Stein beim (freien) Fall nach einer
bestimmten Zeit t zurückgelegt hat, kann man experimentell
bestimmen. Eine Messreihe ergab z.B.:
|
t / s
|
0
|
0,5
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
|
s / m
|
0
|
1,23
|
4,91
|
11,05
|
19,64
|
30,69
|
44,19
|
Wie verhält sich die Fallstrecke s, wenn die Fallzeit verdoppelt
(verdreifacht, vervierfacht, ...) wird?
Jeder Zeit ist genau eine Fallstrecke zugeordnet. Die Zuordnung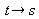 ist
also eine Funktion.
ist
also eine Funktion.
Wie lautet die Funktionsgleichung für s(t)?
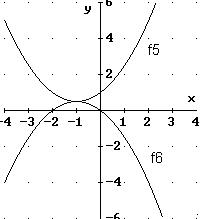
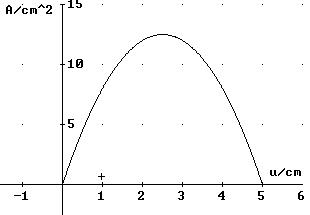
3. In ein Quadrat der Seitenlänge a = 5 cm ist gemäß
der Zeichnung ein Rechteck einbeschrieben.
Für welchen Wert von u wird die Rechteckfläche
am größten?
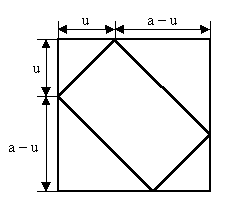
Die Rechteckfläche ergibt sich aus der Quadratfläche, wenn
man die vier entstehenden Dreiecke abschneidet. Je zwei der vier Dreiecke
ergänzen sich zu einem Quadrat, so dass für die Rechteckfläche
folgt:
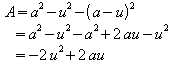
Jedem u ist genau ein Wert A(u) zugeordnet. Die
Zuordnung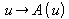 ist
also eine Funktion. Ihre Definitionsmenge ist das Intervall [0 ; 5], denn
u
kann nicht kleiner als Null und nicht größer als 5 werden.
ist
also eine Funktion. Ihre Definitionsmenge ist das Intervall [0 ; 5], denn
u
kann nicht kleiner als Null und nicht größer als 5 werden.
|
u / cm
|
A / cm²
|
|
0
|
0
|
|
0,5
|
4,5
|
|
1
|
8
|
|
1,5
|
10,5
|
|
2
|
12
|
|
2,5
|
12,5
|
|
3
|
12
|
|
3,5
|
10,5
|
|
4
|
8
|
|
4,5
|
4,5
|
|
5
|
0
|
|
|
Die Wertetabelle und der Graph von A lassen vermuten, dass
die Rechteckfläche für u = 2,5 cm am größten
wird.
4. In das Quadrat von Beispiel 3 soll nun ein zweites Quadrat
einbeschrieben werden.
Wie ist u zu wählen, damit die Fläche des einbeschriebenen
Quadrates möglichst klein wird?
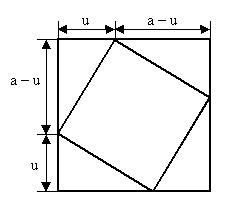
(Wenn Sie gar keine Idee haben, können Sie mit einem Klick auf die
folgenden Schaltflächen immer weiter reichende Tipps erhalten.)
Die in den Beispielen auftretenden Funktionen sind quadratische Funktionen.
Definition: Eine Funktion 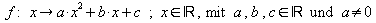 heißt
quadratische
Funktion. Der Graph einer quadratischen Funktion heißt
Parabel. heißt
quadratische
Funktion. Der Graph einer quadratischen Funktion heißt
Parabel. |
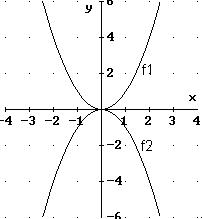
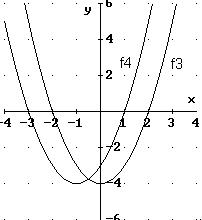
Weitere Beispiele für quadratische Funktionen:
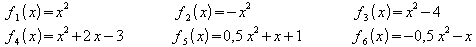
Die Graphen zeigen:
-
Parabeln können nach oben geöffnet oder
nach unten
geöffnet sein;
-
eine Parabel besitzt einen tiefsten oder höchsten Punkt, der Scheitelpunkt
genannt wird;
-
eine Parabel besitzt eine Symmetrieachse: diese ist eine Parallele
zur y-Achse und verläuft durch den Scheitelpunkt der Parabel.
Übung:
Zeichnen Sie die Graphen der folgenden quadratischen Funktionen und
bestimmen Sie den Scheitelpunkt.
Zum Zeichnen können Sie das Applet verwenden, das mit einem Klick
auf die folgende Schaltfläche gestartet wird. Bei der Eingabe von
Werten beachten Sie bitte, dass ein Dezimalpunkt statt eines Kommas
einzugeben ist.
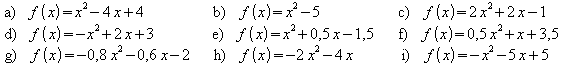
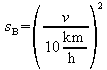 .
.![]() ist
also eine Funktion; ihre Definitionsmenge ist das Intervall [0 ; vmax],
wobei vmax die Höchstgeschwindigkeit des Fahrzeugs
bezeichnet. Werden die Wertepaare (v ; sB) in
ein Koordinatensystem eingetragen, kann der Graph der Bremsweg-Funktion
gezeichnet werden.
ist
also eine Funktion; ihre Definitionsmenge ist das Intervall [0 ; vmax],
wobei vmax die Höchstgeschwindigkeit des Fahrzeugs
bezeichnet. Werden die Wertepaare (v ; sB) in
ein Koordinatensystem eingetragen, kann der Graph der Bremsweg-Funktion
gezeichnet werden.